The Modeling Limitations of Linear Regression Which Poisson Regression Addresses

Linear regression comes with its own set of challenges/assumptions.

For instance:

• After modeling, the output can be negative for some inputs.

• But this may not make sense at times — predicting the number of goals scored, number of calls received, etc.

• Thus, it is clear that it cannot model count (or discrete) data.

Furthermore, in linear regression:

• Residuals are expected to be normally distributed around the mean.

• Hence, the outcomes on either side of the mean (m-x, m+x) are equally likely.

For instance:

• if the expected number (mean) of calls received is 1...

• ...then, according to linear regression, receiving 3 calls (1+2) is just as likely as receiving -1 (1-2) calls. (This relates to the concept of prediction intervals, which I discussed in one of my previous posts here: Prediction intervals.)

• But in this case, a negative prediction does not make any sense.

Thus, if the above assumptions do not hold, linear regression won’t help.

Instead, what you may need is Poisson regression.

Poisson regression:

• is more suitable if your response (or outcome) is count-based.

• assumes that the response comes from a Poisson distribution.

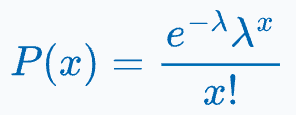
It is a type of generalized linear model (GLM) that is used to model count data.

It works by estimating a Poisson distribution parameter (λ), which is directly linked to the expected number of events in a given interval.

Contrary to linear regression, in Poisson regression:

• Residuals may follow an asymmetric distribution around the mean (λ).

• Hence, outcomes on either side of the mean (λ-x, λ+x) are NOT equally likely.

For instance:

• if the expected number (mean) of calls received is 1...

• ...then, according to Poisson regression, it is possible to receive 3 (1+2) calls, but it is impossible to receive -1 (1-2) calls.

• This is because its outcome is also non-negative.

The regression fit is mathematically defined as follows:

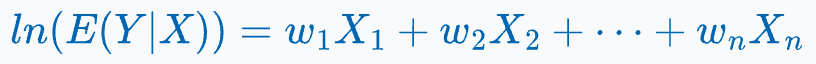
The effectiveness of Poisson regression is evident from the image below:

The following visual neatly summarizes this post:

While this was just about Poisson regression — one of the many members of the generalized linear models (GLMs) family, here’s a deep dive to learn everything about GLMs: Generalized Linear Models (GLMs): The Supercharged Linear Regression.

👉 Over to you: Can you tell me some limitations or considerations for using Poisson regression?

👉 If you liked this post, don’t forget to leave a like ❤️. It helps more people discover this newsletter on Substack and tells me that you appreciate reading these daily insights.

The button is located towards the bottom of this email.

Thanks for reading!

Latest full articles

If you’re not a full subscriber, here’s what you missed:

• DBSCAN++: The Faster and Scalable Alternative to DBSCAN Clustering

• Federated Learning: A Critical Step Towards Privacy-Preserving Machine Learning

• You Cannot Build Large Data Projects Until You Learn Data Version Control!

• Sklearn Models are Not Deployment Friendly! Supercharge Them With Tensor Computations.

• Deploy, Version Control, and Manage ML Models Right From Your Jupyter Notebook with Modelbit

• Gaussian Mixture Models (GMMs): The Flexible Twin of KMeans.

• Bayesian Optimization for Hyperparameter Tuning.

To receive all full articles and support the Daily Dose of Data Science, consider subscribing:

👉 Tell the world what makes this newsletter special for you by leaving a review here :)

👉 If you love reading this newsletter, feel free to share it with friends!